China has had double-digit economic growth for nearly three decades. How can we explain this? In my dissertation, I studied one explanation that is backed up by a large literature: meritocratic promotion. The idea is that politicians compete in promotion tournaments, where the politician with the highest GDP growth rate in their jurisdiction is rewarded by being promoted. By tying promotion to economic growth, meritocratic promotion creates strong incentives to boost GDP, and hence helps explain China’s rapid growth.

When I collected data on prefecture politicians, however, I found no evidence for meritocracy: there was no correlation between GDP growth and promotion, despite trying many different models. How is this null result consistent with the positive findings in the rest of the literature? To find out, I replicated the main papers claiming evidence for prefecture-level meritocracy. Short answer: the literature is wrong.

This post summarizes my replications. I find that the results in the literature are not robust to reasonable specification changes, or are due to data errors. You can find the full details, and a few more replications, in the paper here.

Yao and Zhang (2015)

Yao and Zhang (2015), published in the Journal of Economic Growth, was the first paper to study meritocratic promotion at the prefecture level in China. They estimate a leader’s ability to grow GDP, and then estimate the relationship between ability and promotion. If promotion is meritocratic, we should see a positive correlation, as high-growth leaders are promoted.

However, they find no average correlation between leader ability and promotion: leaders with higher ability are not more likely to be promoted. Despite this, the authors do not frame their paper as contradicting the literature.¹ Moreover, this paper is cited in the literature as supporting the meritocracy hypothesis.²

This is because the authors further test for an interaction between leader ability and age, reporting a positive interaction effect that is significant at the 5% level. Narrowing in on specific age thresholds, they find that leader ability has the strongest effect on promotion for leaders older than 51. They conclude that leader ability matters for older politicians, because more years of experience produces a clearer signal of ability.

Now, this result is consistent with a limited promotion tournament, where the Organization Department promotes older leaders based on their ability to boost growth (because older leaders have clearer signals of ability), but applies different promotion criteria to younger leaders (whose signals are too weak to detect). But this limited model contradicts the usual characterization of China’s promotion tournament as including all leaders, irrespective of age: in each province, leaders compete to boost GDP growth, and the winners are rewarded with promotion.

This is actually a big discrepancy, because half of all promotions occur for leaders younger than 51. If the Organization Department cannot measure ability for these young leaders, what criteria does it use to promote them? Furthermore, remember that the original motivation was to explain China’s rapid growth. The incentives generated by this limited tournament are weaker, since the reward is only applied later in life; if young leaders are impatient, they will discount this future reward and put less effort into boosting growth. The limited tournament model has less explanatory power.

At this point, it is not clear to me why this paper has been cited without qualification as evidence for meritocratic promotion. It offers no general support for meritocracy, and its model of a limited promotion tournament partly contradicts the literature.

But I’m not stopping here. Finding a null average effect with a significant interaction is a classic formula for p-hacked results in social psychology. Since the age interaction doesn’t make much sense, I don’t believe that the authors started out planning to run this test. Rather, it looks like they wanted to find a positive average effect, but didn’t. But they’d already invested a lot of time in collecting the data and working out a clever identification strategy, so they found an interaction that got them statistical significance, even if the interpretation wasn’t really consistent. Hence, I reject their p-value as invalid.³

And it turns out that this is the right call. Digging into the paper, I find that the significant interaction term depends on including questionable control variables.

When estimating leader ability, the authors regress GDP growth on three fixed effects (leader, city, year) as well as three covariates: initial city GDP per capita (by leader term), annual city population, and the annual provincial inflation rate. I think it makes sense to control for initial GDP by term. The model includes city effects, so level differences in growth rates are not an issue. But we might worry that the variance of idiosyncratic shocks to growth is correlated with city size, and growth shocks could affect promotion outcomes.

However, it is not clear why population and inflation should be included. The authors mention that labor migration can drive GDP growth (p.413), but a leader’s policies affect migration, so population is plausibly a collider or ‘bad control’, if leader ability affects growth through good policies that increase migration. The authors provide no justification for including inflation, which is odd because the dependent variable (real per capita GDP growth) is already expressed in real (rather than nominal) terms.

Given the lack of justification for including population and inflation as covariates, I re-estimate leader ability controlling only for initial GDP. Using this new estimate of ability, I then replicate their main results. I again find a nonsignificant average effect of ability on promotion. But now the interaction with age disappears. The sign remains positive, but the magnitude of the coefficient drops by half, and the results are nonsignificant.

So it turns out that Yao and Zhang (2015) offers no evidence for meritocratic promotion of prefecture leaders.

Li et al. (2019)

Li et al. (2019), published in the Economic Journal, studies GDP growth targets and promotion tournaments in China. They start with the observation that growth targets are higher at lower levels of the administration; for example, prefectures set higher targets than do provinces. Their explanation is that the number of jurisdictions competing in each promotion tournament is decreasing as one moves down the hierarchy, which increases the probability of a leader winning the tournament. As a consequence, leaders exert more effort, and higher-level governments can set higher growth targets without causing leaders to quit.

As part of their model, they assume that promotion is meritocratic: performance (measured by GDP growth) increases the probability of promotion. Further, they report an original result: the effect of performance on promotion is increasing in the growth target faced. That is, a one percentage-point increase in growth will increase a mayor’s chances of promotion by a larger amount when the provincial target is higher, relative to when the target is lower.

This result seems naturally testable by interacting \(Growth \times Target\) in a panel regression, with a predicted positive coefficient on the interaction term. However, the authors argue that OLS is invalid, instead reporting results based on maximum likelihood where promotion is determined by a contest success function. Why does OLS not apply? “Standard linear regression does not work here partly because promotion is determined by local officials’ own growth rates as well as by the growth rates of their competitors. The nonlinearity of the promotion function is another factor that invalidates the OLS estimation.” (p.2906)

But these are not problems for OLS. First, as is standard in this literature, the promotion tournament can be captured by using prefecture growth rates relative to the annual provincial growth rate. Second, OLS is the best linear approximation to a nonlinear conditional expectation function. So if there is a positive nonlinear relationship between promotion and growth, we should be expect that it will be detected by OLS.⁴

Given the lack of justification for omitting results from linear regression, I replicate their results using a linear probability model and logistic regression. First, I test the generic meritocracy hypothesis. I find that GDP growth has no average effect on promotion. Next, I do find a positive interaction effect between growth and growth target, but it’s not statistically significant.

This doesn’t look good for the authors. OLS is the default method, and you need a strong justification for not reporting it. But their reasons are flimsy. Now it looks like they tried OLS, didn’t get the result they wanted, then made up a complicated maximum likelihood model that delivered significance.

So Li et al. (2019) is another paper that claims to provide evidence for meritocratic promotion of prefecture leaders, but is unable to back up those claims.

Chen and Kung (2019)

Chen and Kung (2019), published in the Quarterly Journal of Economics, studies land corruption in China, with secondary results on meritocratic promotion. The main result is that local politicians provide price discounts on land sales to firms connected to Politburo members, and these local politicians are in turn rewarded with promotion up the bureaucratic ladder.

For provincial leaders, they find a strong effect of land sales on promotion for secretaries, but not for governors. In contrast, GDP growth strongly predicts promotion for governors, but not secretaries. They conclude that “the governor has to rely on himself for promotion, specifically by improving economic performance or GDP growth in his jurisdiction [...] only the provincial party secretaries are being rewarded for their wheeling and dealing".

They find similar results at the prefecture level: land deals predict promotion for secretaries, but not for mayors, while GDP growth predicts promotion for mayors, but not for secretaries. Overall, this supports the model of party secretaries being responsible for social policy, while governors (and mayors) are in charge of the economy, with performance on these tasks determining promotion. Thus, at both province and prefecture levels, government leaders (governors and mayors) compete in a promotion tournament based on GDP growth, while party secretaries do not.

However, Chen and Kung (2019)’s results for prefecture mayors are questionable, because their promotion data seems wrong. In my data, the annual promotion rate varies from 5 to 30% (peaking in Congress years), while the Chen and Kung (2019) data never exceeds 15% and has six years where the promotion rate is less than 2%. Figure 1 compares the annual promotion rate from Chen and Kung to my own data as well as the data from Yao and Zhang (2015) and Li et al. (2019), where each paper uses a binary promotion variable (and data on prefecture mayors). While the latter three sources broadly agree on the promotion rate, the Chen and Kung data is a clear outlier. This is obviously suspect.

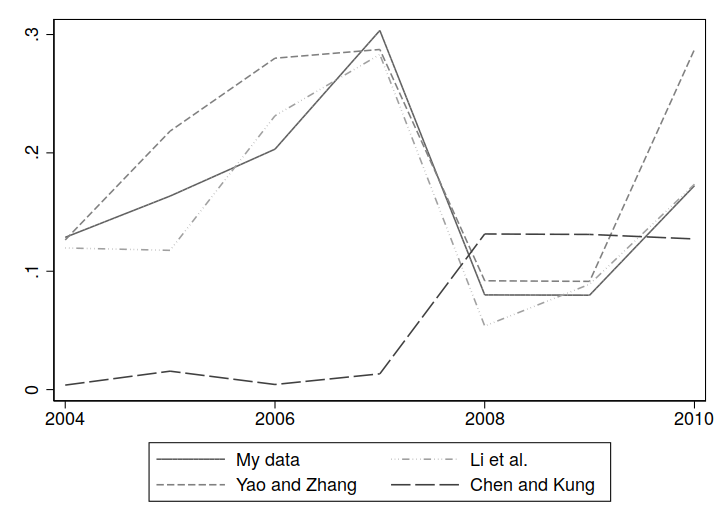
Furthermore, upon investigating this discrepancy, I discovered apparent data errors in their promotion variable. The annual promotion variable is defined to be 1 in the year a mayor is promoted, and 0 otherwise. However, out of the 201 cases with \(Promotion=1\), 124 occur before the mayor’s last year in office (with the remaining 77 cases occuring in the last year). Moreover, this variable is equal to 1 multiple times per spell in 4% of leader spells. Out of 1216 spells, 51 spells have \(Promotion=1\) more than once per spell. For example, consider a mayor who is in office for five years and then promoted; the promotion variable should be 0 in the first four years, then 1 in the final year. However, the Chen and Kung data has spells where the promotion variable is, for example, 0 in the first two years, and 1 in the final three years.

To fix this error, I obtained the raw mayor data from James Kung, and used it to generate a corrected annual promotion variable, which is 1 only in a mayor’s final year in office (when the mayor is promoted). This data-coding error more than doubles the number of promotions. But since the Chen and Kung promotion rate is smaller than the rest of the literature, fixing the data errors in fact makes the disagreement with the literature even more pronounced.

So this promotion data looks pretty lousy. Naturally, we should worry that their data is driving their finding of meritocratic promotion for prefecture mayors. To test this, I re-run their analysis using my own promotion data. I find that the correlation between GDP growth and promotion is now negative and nonsignificant. So just like the other two papers, Chen and Kung (2019) also fails to provide evidence for meritocratic promotion of prefecture leaders.

This is extremely suspicious. Speculating, it looks like the authors had a nice paper using provincial data, but a referee asked them to extend it to prefecture leaders. To fit their story, they needed to find an effect of land sales for secretaries (but not mayors), and an effect of GDP growth for mayors (but not secretaries). But maybe the data didn’t agree, and their RA had to falsify the mayor promotion data to get the ‘correct’ result. This wouldn’t be easy for referees to spot, since the replication files didn’t include spell-level data. But how else did they collect such error-ridden data that also just happened to produce results consistent with their story?

Conclusion

The original study of meritocratic promotion for provincial leaders, Li and Zhou (2005), has been cited over 2500 times. But follow-up work has repeatedly failed to confirm its finding of a positive correlation between provincial GDP growth and promotion.⁵ And as I have shown in this post, attempts to extend the meritocracy story down to prefecture leaders have also failed.

How did this happen? How could a whole literature get this wrong?

Here’s my guess: researchers set a strong prior based on the provincial result in Li and Zhou (2005), combined with the elegance of the theoretical model of a promotion tournament. Since the idea of a promotion tournament is generic, researchers naturally expected it to apply to prefecture and county politicians as well. In short, researchers doing follow-up work knew that they had to confirm the original results.

However, when they studied prefecture leaders and didn’t find a positive correlation between growth and promotion, the researchers had to fiddle around with their models and data until they got a result that matched the original. And given the multiplicity of design choices⁶, it wasn’t that difficult to find a specification that yielded statistical significance.

But why not embrace the null result and contradict the literature? After all, this is a case where a null result would be interesting, with adequate statistical power and a well-established consensus. I guess it was just easier to shoehorn their results to fit in with the literature, and get the publication, rather than challenge the consensus.

My conclusion is that publication incentives, conformism, and inadequate peer review led to a literature of false results.

Footnotes

Read the full paper here. My null result paper is here.